서론
구현 2번째 문제이다. 이번 문제는 dx dy 방향벡터를 활용해서 문제를 풀어보도록 하겠다.
본론
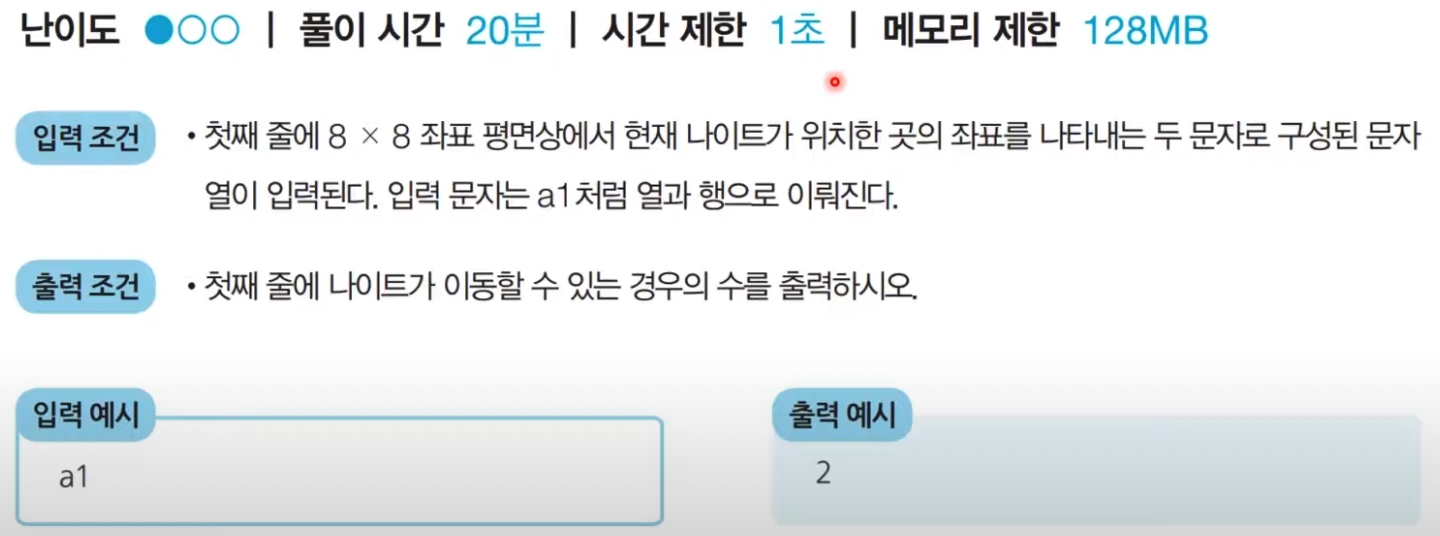

1) a -> 1, b->2 ... h->8 으로 해석할 수 있겠구나!
이를위해 ord()함수를 써서 문자열을 아스키 코드로 바꿔서 행렬계산해보자(*chr()은, 숫자를 아스키코드로 바꾸는데 사용)
def kingKnight(S):
x = ord(S[0]) - 96
y = int(S[1])
cnt = 0
if x - 2 > 0 and y - 1 > 0:
cnt+=1
if x - 2 > 0 and y + 1 > 0:
cnt += 1
if x + 2 > 0 and y - 1 > 0:
cnt += 1
if x + 2 > 0 and y + 1 > 0:
cnt += 1
if x - 1 > 0 and y - 2 > 0:
cnt += 1
if x - 1 > 0 and y + 2 > 0:
cnt += 1
if x + 1 > 0 and y - 2 > 0:
cnt += 1
if x + 1 > 0 and y + 2 > 0:
cnt += 1
return cnt
print(kingKnight('a1'))
print(kingKnight('c2'))반성할점: 수많은 if문도 타인이 코드 이해하는 면에서 나쁘진않은데, 좌표값을 활용해서 코드를 단축시켜보자
def kingKnight_refactoring(S):
x = ord(S[0]) - 96
y = int(S[1])
cnt = 0
move =[[-2,-1],[-2,1],[2,-1],[2,1]]
for m in move:
if x + m[0] > 0 and y + m[1] > 0:
cnt += 1
if x + m[1] > 0 and y + m[0] > 0:
cnt += 1
return cnt
print(kingKnight_refactoring('a1'))
print(kingKnight_refactoring('c2'))반성할점: 8x8인데 이점을 제대로 파악 못하고 계산했다.
def kingKnight_dongbinna(S):
x = ord(S[0]) - ord('a') + 1
y = int(S[1])
move =[(-2, -1), (-2, 1), (2, -1), (2, 1), (-1, 2), (-1, -2), (1, 2), (1, -2)]
cnt = 0
for m in move:
new_x = x + m[0]
new_y = y + m[1]
if new_x >= 1 and new_x <= 8 and new_y >= 1 and new_y <= 8:
cnt += 1
return cnt
print(kingKnight_dongbinna('a1'))
print(kingKnight_dongbinna('c2'))배운점: 타인이 코드를 봤을때, x값에서 -96을 한게 뭔소린지 모를만하다. ord('a')하는게 타인이 보았을때 더 이해하기 쉬울것이다.
또한 리스트아넹 리스트보다는 수정이 불가능한 튜플을 사용하는것이 좀 더 좋을것같다.
마무리
속도면에서 많이 발전했다.
다만, 코드 시안성까지는 바라지 않더라도 반례에 대해서 좀 더 깊은 생각이 필요해보인다.
꾸준히 잘하고 있다.
'Algorithm > Problem Solving' 카테고리의 다른 글
| [한개라도 제대로] DFS&BFS(1) - 백준 2178번 미로 탐색 (0) | 2022.02.01 |
|---|---|
| [한개라도 제대로] 구현(3) (0) | 2022.01.13 |
| [하나라도 제대로] 구현(1) (0) | 2022.01.09 |
| [하나라도 제대로] 그리디알고리즘(3) (0) | 2022.01.07 |
| [하나라도 제대로] 그리디알고리즘(2) (0) | 2022.01.06 |